Daten beschreiben Eigenschaften von Produkten, Prozessen oder Dienstleistungen. Diese Eigenschaften können in qualitative und quantitative Daten unterteilt werden. Zur datenbasierenden Analyse im Lean Six Sigma sollten die folgenden Datentypen und Verteilungen bekannt sein.

Bestimmen Sie das Merkmal und die Merkmalsausprägungen. Z.B. Merkmal = Alter; Merkmalsausprägung = 42 Jahre.
Die Merkmalsausprägungen müssen in eine Skala gesetzt werden, um den Datentyp zu definieren.
| Skala | Merkmalausprägungen | Beispiele |
|---|---|---|
| Nominal | Rein qualitativ ohne Ordnung | Geschlecht, Berufsstand, Farben |
| Ordinal | Qualitativ mit natürlicher Ordnung | Noten, Rang beim Militär |
| Metrisch | Quantitativ (zählbar/messbar) | 10 Fehler, Luftdruck, Temperatur |
Nach der Identifizierung der Daten können diese mit der Statistik ausgewertet werden.
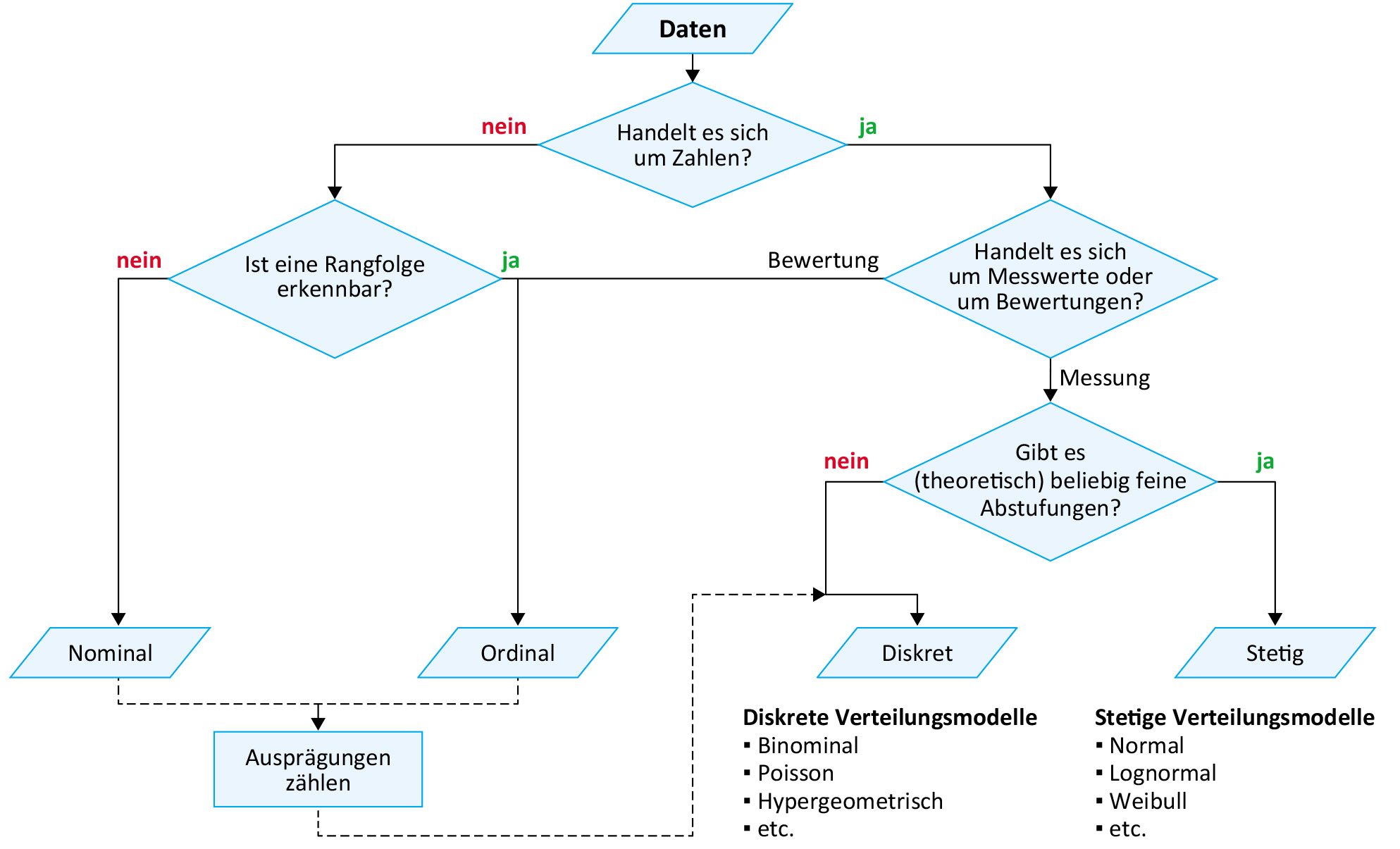
Verteilungen werden in der Statistik üblicherweise durch Funktionen beschrieben. Es existieren Modelle (Formen) für stetige und für diskrete Verteilungen.
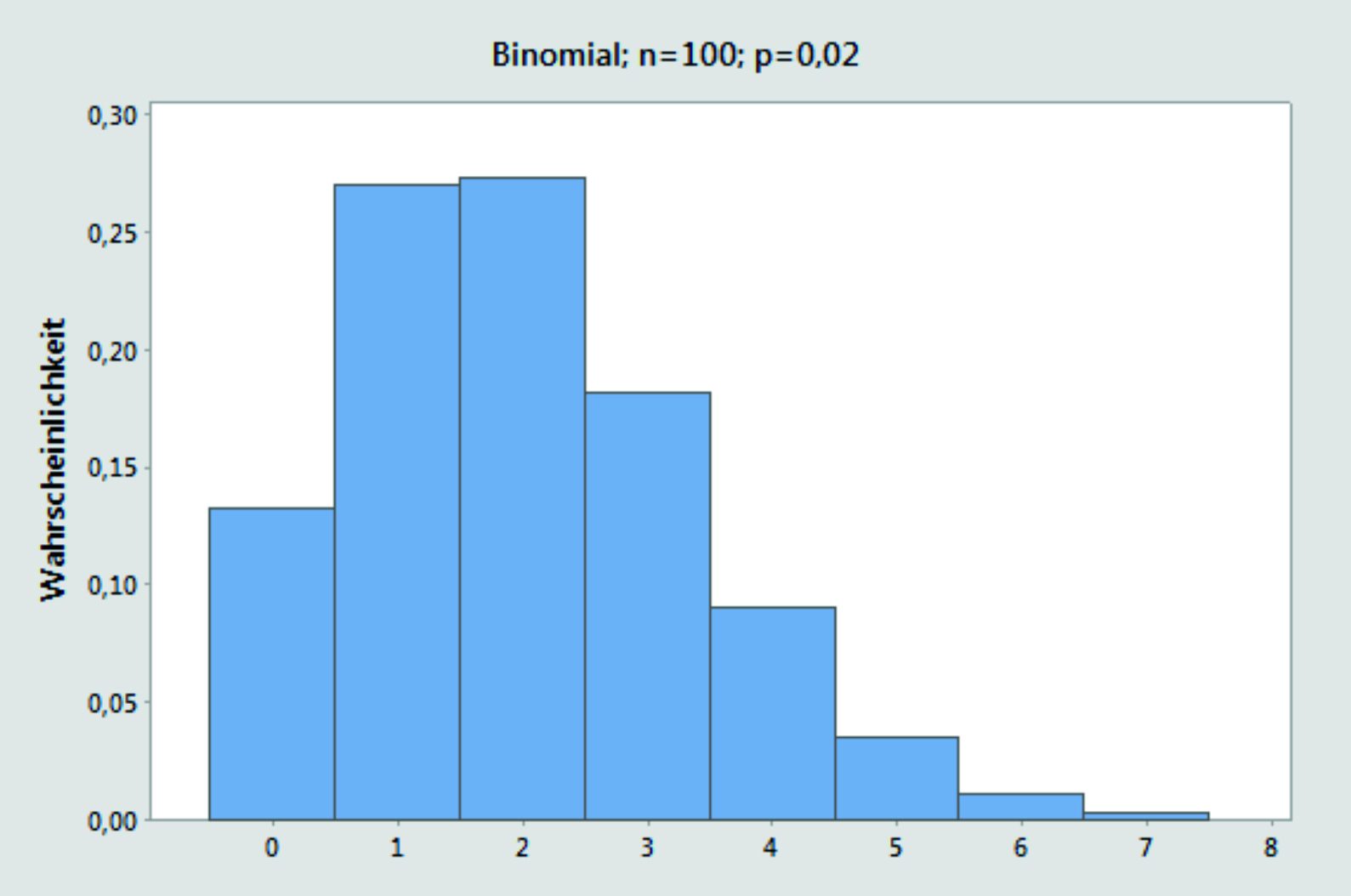
Die Binomialverteilung ist eine diskrete Verteilungen. Mit ihr kann man die Häufigkeit von Merkmalen, in zwei Ausprägungen darstellen. Z.B. Anzahl Fehler in einer Produktion.
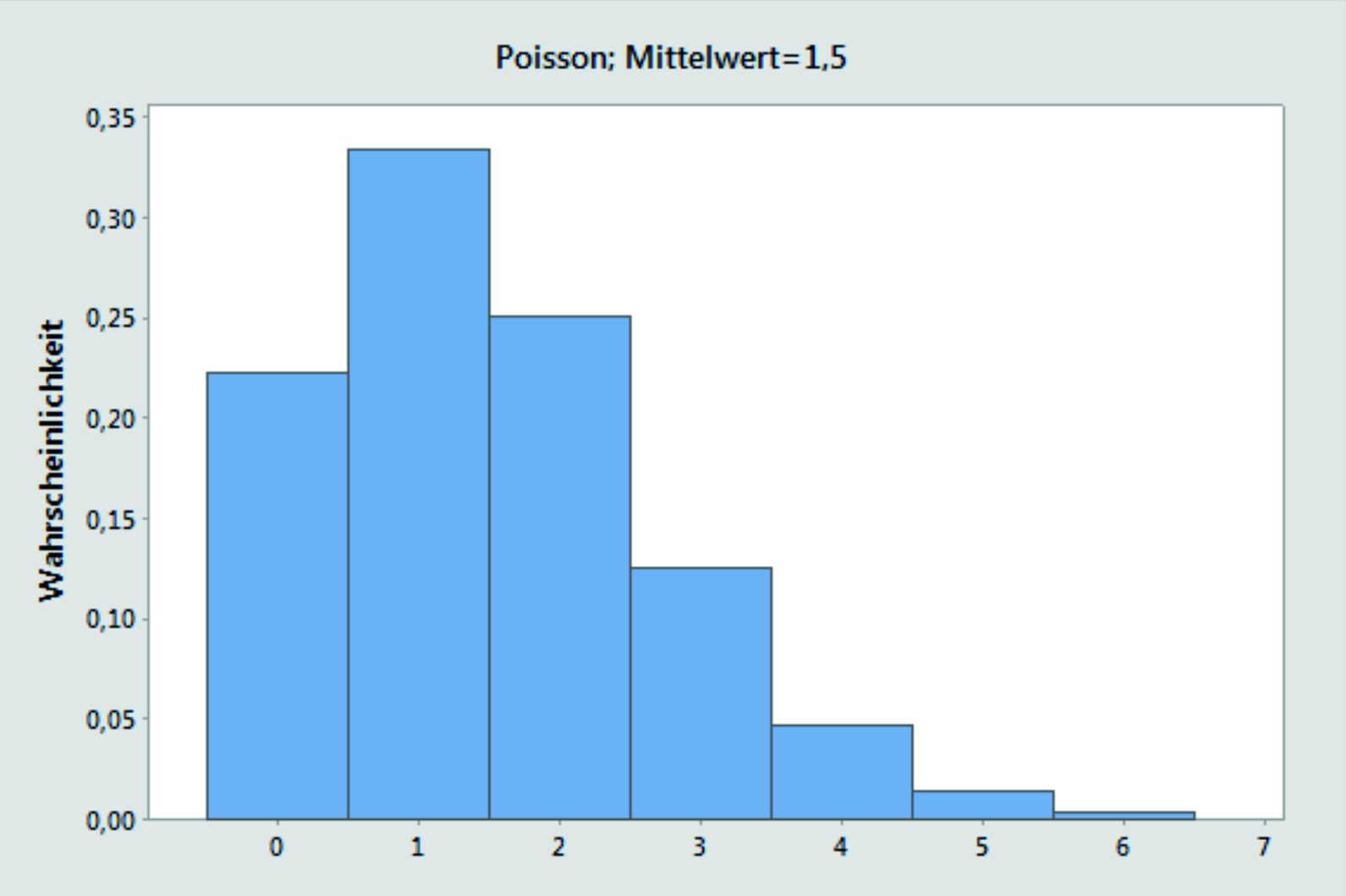
Die Poissonverteilung ist ein spezieller Fall der Binomialverteilung.
Mit ihr werden die Anzahl der Fehler pro Einheit beschrieben, die in einer Einheit vorkommen.
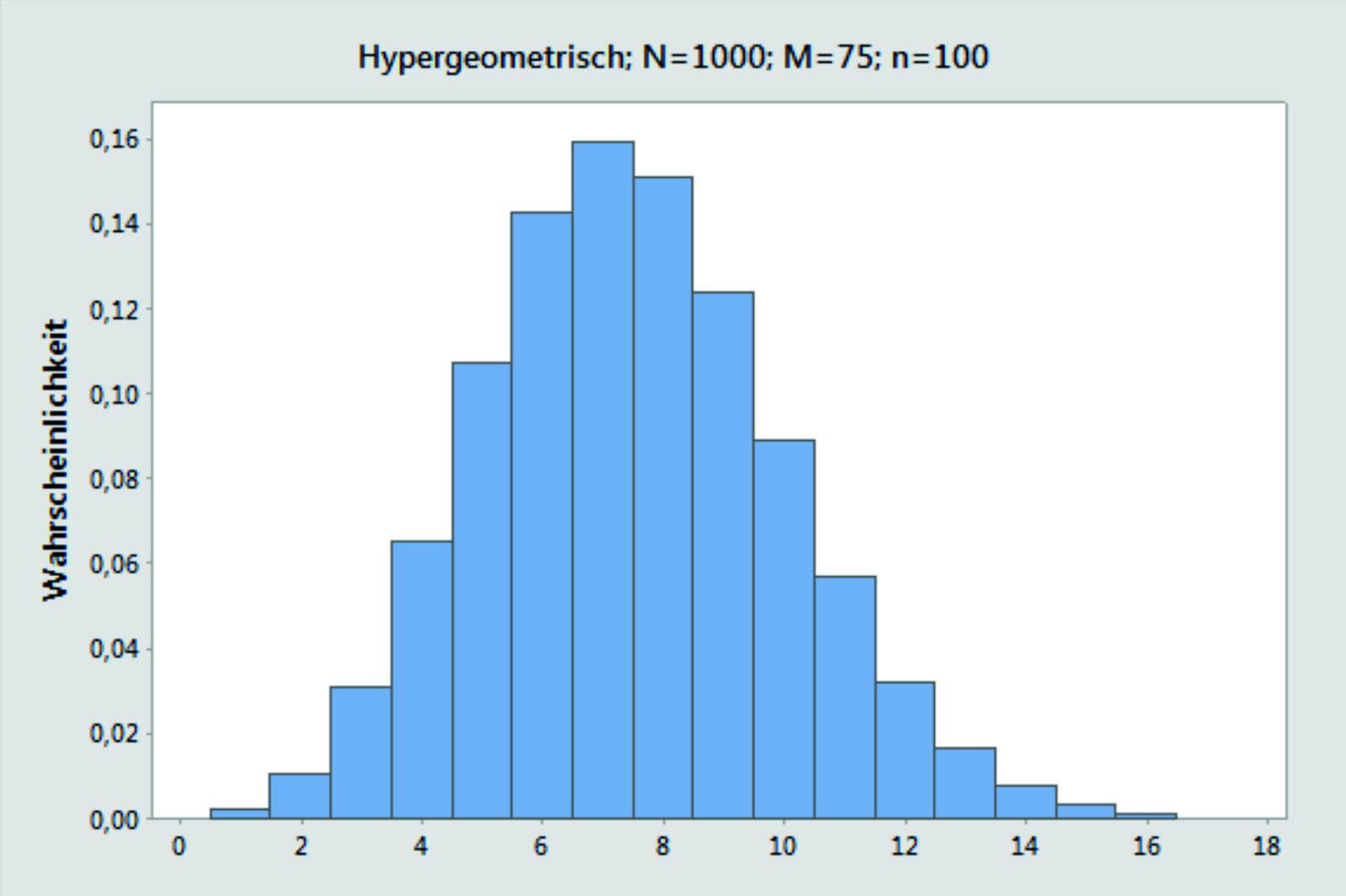
Die Hypergeometrische Verteilung wird verwendet, wenn die Stichproben aus kleinen Grundgesamtheiten ohne Zurücklegen gezogen werden. Ein Beispiel sind die Lottozahlen.
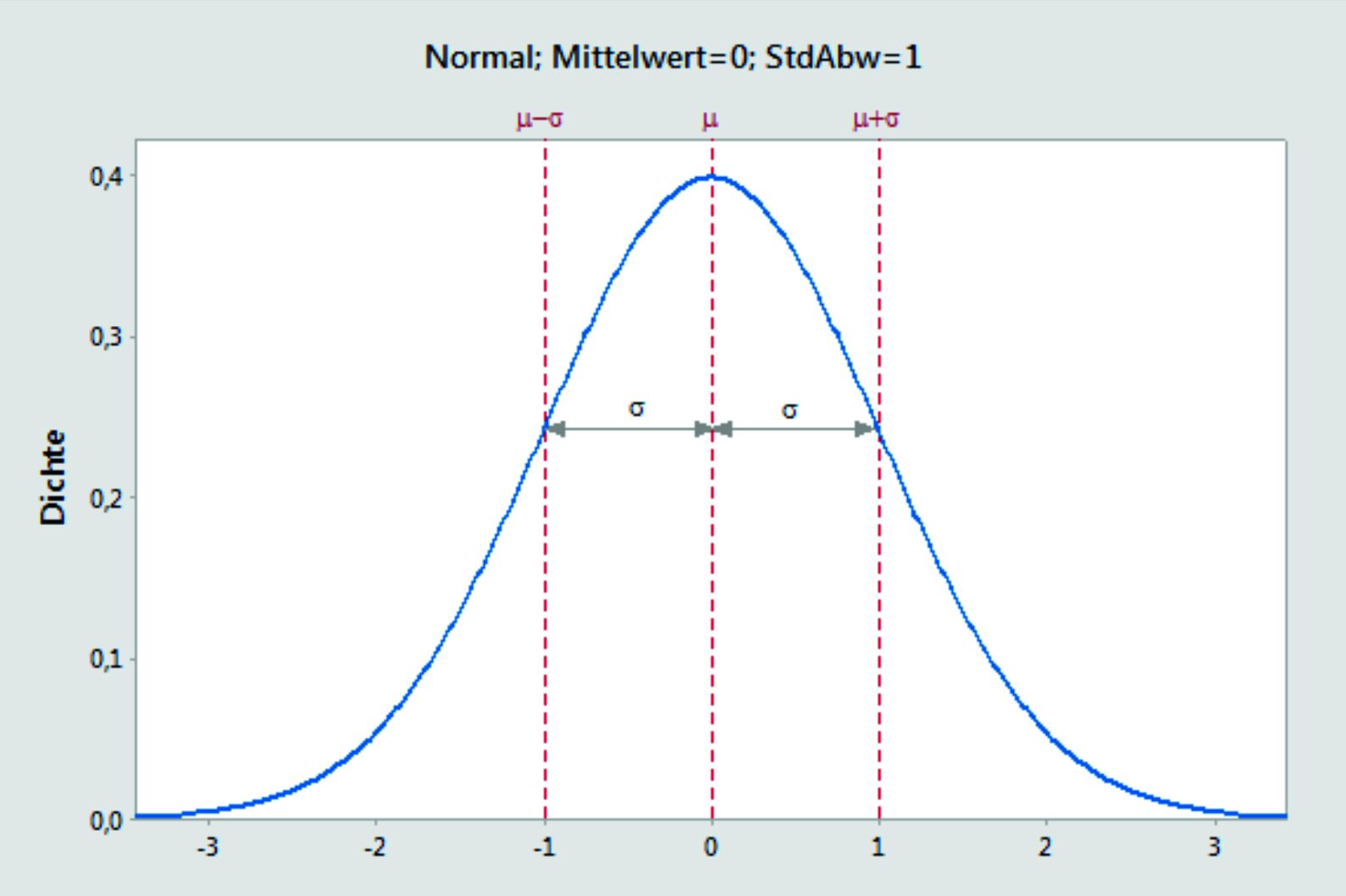
Die Normalverteilung ist die wichtigste Verteilungsfunktion für stetige Daten. Die meisten statistischen Verfahren basieren auf normalverteilten Daten.
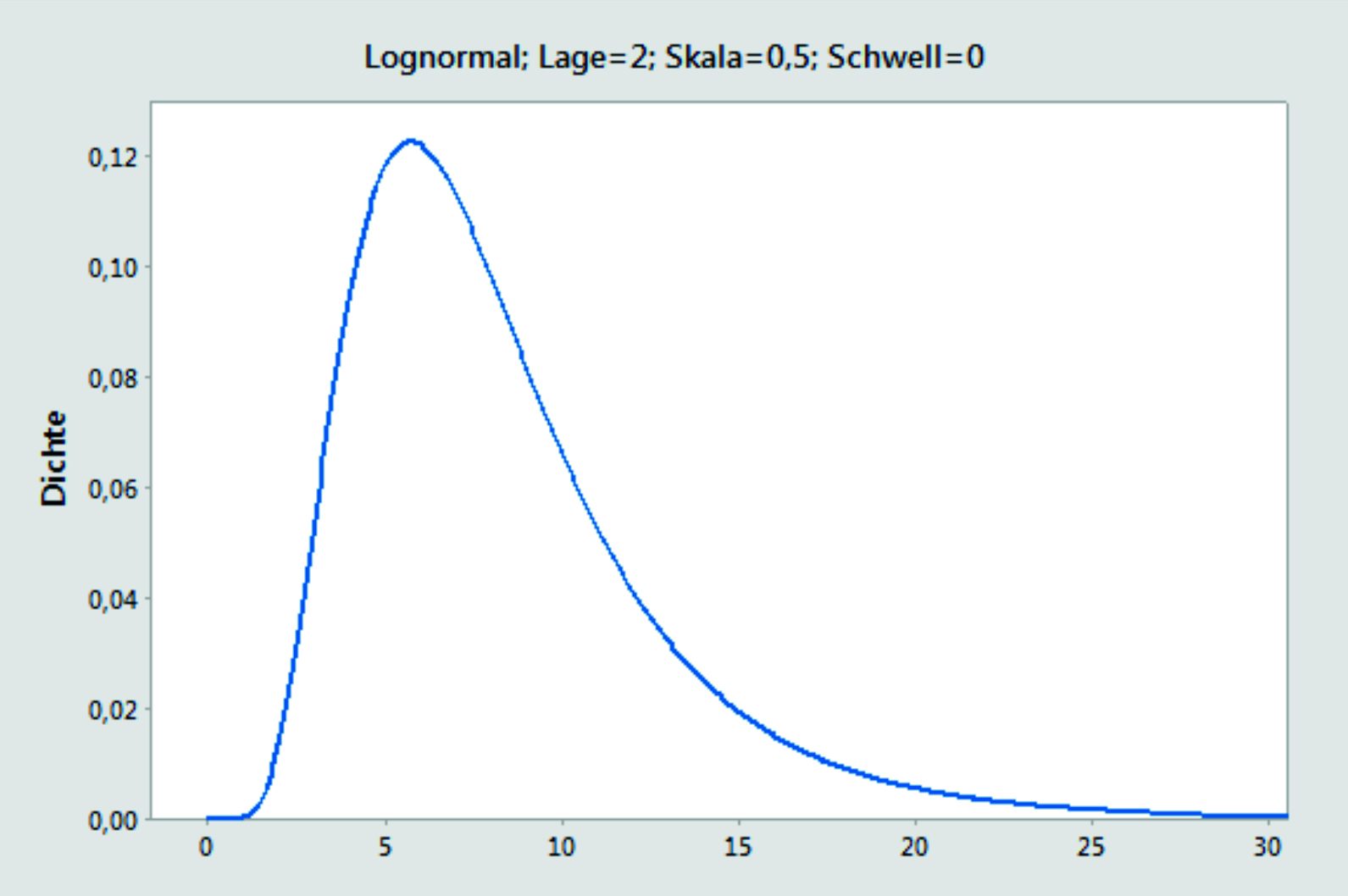
Die Lognormalverteilung ist linkssteil und rechtsschief und nimmt keine Werte kleiner als 0 an. Sie wird häufig angewendet, um Prozesszeiten zu beschreiben.
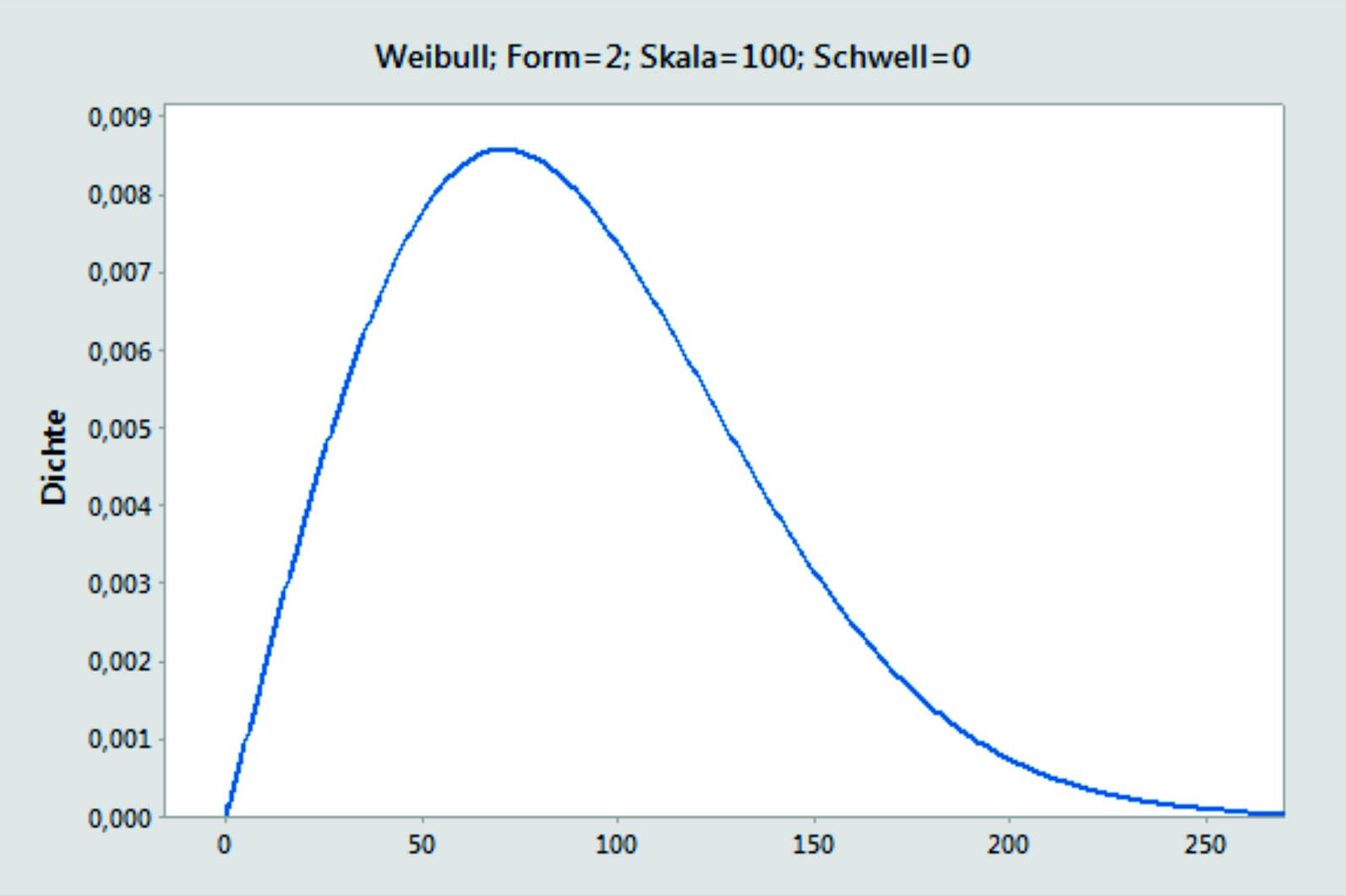
Die Weibullverteilung ist in ihrem Verlauf sehr flexibel. Über die Parameterwerte kann die Kurve an verschiedene Verläufe angepasst werden. Beispiele sind Lebensdaueranalysen.

Mit mehr als 4.000 Projekten und Fallstudien ist die Firma Alphadi führend im Bereich Lean Six Sigma sowie Sales Process Engineering. Wir beraten Sie ganzheitlich, damit Ihre Ziele nachhaltig und langfristig erreicht werden.
2024 © All Rights Reserved.